Sequencer identifies number sequences. That is, given a list of numbers like
$$(a_n)_{n\geq 1} = 1,; 2,; 4,; 8,; 16,; 32,; \ldots$$
it finds a formula that generates them, in this case
$$a_n = 2^{n-1}$$
Sequencer employs neither a library of sequences nor a limited set of algorithms to find a closed form. Instead, it generates all formulas up to a certain size and then checks them against the provided numbers.
For verification, the system uses a hybrid approach of a fast numerical checker followed by a symbolic verifier powered by the Symja computer algebra system. Coupled with some tricks and heuristics designed to quickly generate potentially interesting formulas, Sequencer can identify sequences with very complex closed forms in a matter of seconds when run on commodity hardware.
Sequencer is capable of finding closed forms that are beyond any existing system like OEIS, Superseeker and Wolfram Alpha. It is particularly strong where recurrence relations or unusual combinations of functions are involved. For example, none of the services mentioned above can currently make sense of the sequence
$$(a_n)_{n\geq 1} = 1,; 1,; 1,; 3,; 5,; 15,; 43,; 273,; \ldots$$
while Sequencer reveals that it satisfies the recurrence relation
$$
\begin{align}
a_1 &= 1 \\
a_2 &= 1 \\
a_3 &= 1 \\
a_n &= a_{n-2}^2+a_{n-1}+a_{n-3}\quad \text{for } n\geq 4
\end{align}
$$
and provides the continuation
$$2137,; 76709,; 4643751,; 5888916569,; 21570312343279,; \ldots$$
Web service "SequenceBoss"
For quick access to Sequencer's capabilities from anywhere, I have deployed a web application called SequenceBoss (http://sequenceboss.org).
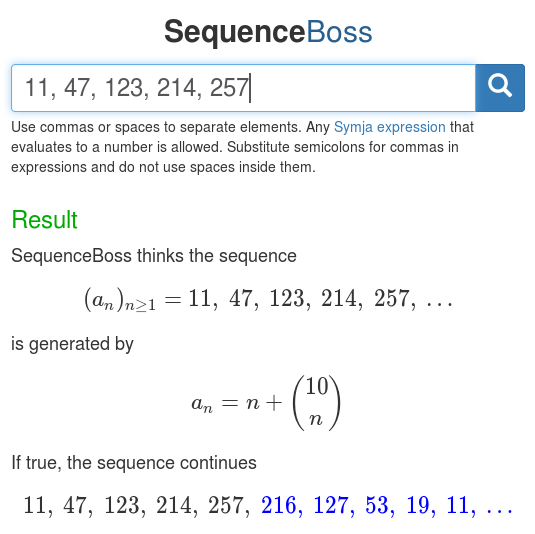
SequenceBoss invokes Sequencer on the numbers entered (with limited search depth) and renders the result in $\LaTeX$ using MathJax. It has a responsive HTML interface that works well on both desktops and mobile devices and is the easiest way to use Sequencer.
Command line
For maximum portability and power, Sequencer is distributed in the form of a JAR that can be run from the command line on any platform with a JRE using the syntax
java -jar sequencer.jar 1 2 3 4 5
Sequencer supports many command line options to fine-tune how searches are performed. As of version 1.5.0, the full list is
-d <value> | --depth <value>
search depth (maximum number of nodes in expression tree) [default: 6]
-r <value> | --results <value>
maximum number of formulas to return, 0 for unlimited [default: 5]. Note that for parallel searches, the order in which formulas are found is not deterministic so limiting the number of search results can lead to unreproducible searches unless the --sequential option is also used.
-p <value> | --predict <value>
number of elements to predict in sequence continuation [default: 5]
-u <value> | --recurrence-depth <value>
maximum number of previous elements to consider for recurrence relations [default: 3]
-c | --no-combinatorics
do not search for combinatorial functions (speeds up search)
-n | --no-number-theory
do not search for number theoretic functions (speeds up search)
-t | --no-transcendentals
do not search for transcendental functions (speeds up search)
-q | --sequential
disable search parallelization (single-threaded search)
-s | --symbolic
skip numerical test (symbolic verification only; slows down search)
-o | --hide-progress
do not output progress while searching
-l | --latex
output LaTeX instead of plain text
Symbolic input and output
Sequencer is not limited to processing integers but can identify sequences consisting of arbitrary Symja expressions (provided they can be evaluated numerically). For example, invoking the program with the arguments 0 1/2 sqrt(3)/2 1 produces
a(n) = Sin(1/6*Pi*(n-1))
Continuation: 1/2*3^(1/2), 1/2, 0, -1/2, (-1/2)*3^(1/2), ...
Note that parentheses in arguments need to be escaped (\() when running a program from a shell like bash.
Cover image: Nevit Dilmen (Wikimedia Commons, CC-BY-SA)
